6  Probability and statistics

In this chapter we will show various visualizations and Python basics of concepts we have seen in the course Probability and Statistics (35B402).

More precisely, this chapter consists of two parts: links to interactive applications illustrating concepts and examples seen in class, and Python basics for working with probability distributions and randomly generated data.

Note

This document will be updated throughout the course Probabilisty and Statistics during the academic year 2025/2026.

6.1 Probability distributions

The stats module of SciPy has many built-in probability distributions. Each distribution can be seen as an object on which various methods can be performed (such as accessing its probability density function or summary statistics like the mean and median).

import numpy as np
import scipy.stats as stats

In this section we will focus on continuous probability distributions. SciPy also has many built-in discete probability distributions.

A list of all continuous distributions that are present in the stats module can be found here; they are so-called stats.rv_continuous objects. Assuming that SciPy’s stats package in import under the alias stats, we can instantiate a distributional object by using stats.dist_name where dist_name is the name of a built-in (continuous) probability distribution in the mentioned list.

Many distributions have input parameters scale and loc that model the scale and location of the distribution, respectively. Depending on the distribution that is considered, these parameters have different meanings.

As an example, the normal distribution has probability density function f(x) = \frac{1}{\sqrt{2\pi\sigma^2} } e^{-\frac{(x-\mu)^2}{2\sigma^2}} which is parameterized by \mu and \sigma.

In Python \mu is the loc parameter, and \sigma the scale parameter. To figure out the function of the scale and loc parameter, you can check the documentation (which can be found here for the Normal distribution).

Documentation of the normal distribution

All distributions have default values for these parameters, which are typically loc=0 and scale = 1.

# Create normal distribution object with mu=0, sigma=1
dist_norm = stats.norm(loc=0, scale=1)

Once a distribution object has been instantiated, we can use methods (i.e., functions) to obtain various properties of the distribution, such as its probability density function (pdf), cumulative density function (cdf) and summary statistics such as the mean, variance and median (or, more general, quantiles).

We give a list of some common methods for a distribution object named dist_name. We start with common functions associated with a probability distribution.

• dist_name.pdf(x): Value f(x) where f is the pdf of the distribution.
• dist_name.cdf(x): Value F(x) where F is the cdf of the distribution.

x = 1
print(dist_norm.pdf(x))

0.24197072451914337

All the above functions are vectorized, meaning here that they can also take one-dimensional Numpy arrays as input, in which case they return the requested value for every element in the array.

x = np.array([1, 3, 5.5])
print(dist_norm.pdf(x)) # Gives probability density function evaluated in x = 1, 3, 5.5

[2.41970725e-01 4.43184841e-03 1.07697600e-07]

We can also access various summary statistics:

• dist_name.mean(): Returns mean of the distribution
• dist_name.var(): Returns variance of the distribution
• dist_name.median(): Returns median of the distribution

dist_norm = stats.norm(loc=0,scale=2)

mean =  dist_norm.mean()
variance = dist_norm.var()
median = dist_norm.median()

print("Mean of the distribution is", mean)
print("Variance of the distribution is", variance)
print("Median of the distribution is", median)

Mean of the distribution is 0.0
Variance of the distribution is 4.0
Median of the distribution is 0.0

As a final application of density functions, we show how they can be used to compute convolutions.

Insight 3.19: Convolution of three distributions

Following the setting of Insight 3.19 seen in class, let Z = X + Y + U with X \sim \text{LogNormal}(\mu,\sigma^2), Y \sim \text{Exp}(\lambda) and U \sim U(a,b), that is, Z is the sum of a log-normal, exponential and uniform distribution.

The goal is to create for a grid of z-values, the corresponding probability density f_Z(z)-values. Computing convolutions can be done easily with the convolve() function from SciPy’s signal package. In the code below this is done in a two-step approach, which we will first elaborate on.

First, the pdf of W = X + Y, f_{W}(w) = \int_{-\infty}^{\infty}f_X(x)f_Y(w-x) \mathrm{dx}, of the convolution of X and Y is computed for various values of w, and then afterwards the pdf f_Z = F_{(X+Y) + U} as the convolution of W = X+Y and U is computed in a similar way.

Because we cannot compute the integral above analytically, we approximate it by a discrete sum over a finite range of x-values. In the code below, we take the discretized grid D = \{0,001,002,\dots,19.999,20\} of x-values with now the interpretation that \mathrm{dx} = 0.001, so that the discrete approximation becomes f_{X+Y}(w) \approx \sum_{x \in D} f_X(x) f_Y(w-x) \mathrm{dx}.

To quickly compute the grid values, we can use the arange() function from NumPy. For three inputs a, b and \text{step} this function returns a NumPy array with the values [a, a + \text{step}, a + 2\cdot \text{step},\dots, b - \text{step}]. Note that the value of b itself is excluded. Let us illustrate this with an example.

a = 2
b = 5
step = 0.2

x = np.arange(a,b,step)

print(x)

[2.  2.2 2.4 2.6 2.8 3.  3.2 3.4 3.6 3.8 4.  4.2 4.4 4.6 4.8]

To compute \sum_{x \in D} f_X(x) f_Y(w-x) \mathrm{dx}, we evaluate the probability density function of the distributions of X and Y in the grid points in x in the code below and store these in f_X and f_Y. The function convolve() then computes the quantity \sum_{x \in D} f_X(x) f_Y(w-x) for many values of w (explained below). To obtain the approximation for f_{X+Y}(w) we have to multiply this expression by \mathrm{dx}, which can be considered a constant in the discrete approximation.

Because we evaluate f_X and f_Y on the domain D, all the values that the sum W = X + Y can attain are in the set \{0,001,002,\dots,19.999,20,20.001,\dots,39.999,40.000\}. The elements in f_W correspond to f_W(w) for the w’s in this set. We compute these w-values as well for completeness.

The above steps are then repeated for the second convolution. The final z-values, for which f_Z(z) has been computed and stored in f_Z, are computed in the array z.

Although this is not a complete description of what is going on in the code below, it does illustrate that convolutions can be numerically computed with relatively small (programming) effort as opposed to a typically hard analysis of the corresponding integral analytically.

import numpy as np
import scipy.stats as stats
from scipy.signal import convolve

# Parameters (as in Insight 3.19)
mu = 0.0
sigma = 0.5
lam = 1.0
a, b = 0.0, 2.0

# Grid D (create with built-in function np.arange())
dx = 0.001
x_max = 20
x = np.arange(0, x_max + dx, dx) 

# PDFs
f_X = stats.lognorm.pdf(x, s=sigma, scale=np.exp(mu))
f_Y = stats.expon.pdf(x, scale=1/lam)
f_U = stats.uniform.pdf(x, loc=a, scale=b - a)

# First convolution: W = X + Y. 
f_W = convolve(f_X, f_Y, mode="full") * dx

# Corresponding grid for W
w = np.arange(0, len(f_W)) * dx

# Second convolution: Z = (X + Y) + U = W + U: 
f_Z = convolve(f_W, f_U, mode="full") * dx

# Corresponding grid for Z
z = np.arange(0, len(f_Z)) * dx

In the code above the final array z contains various values so thatf_Z[i] is the pdf value of Z of the i-th element z[i] in z. We can also visualize the resulting pdf by plotting z against f_Z.

If you want to know more about plotting functions with Python, you can have a look, e.g., here .

import matplotlib.pyplot as plt

# Plot
plt.figure(figsize=(8, 4))
plt.plot(z, f_Z, label="PDF of Z = X + Y + U")
plt.xlim(0, 15)
plt.xlabel("z")
plt.ylabel("Density")
plt.legend()
plt.grid()
plt.show()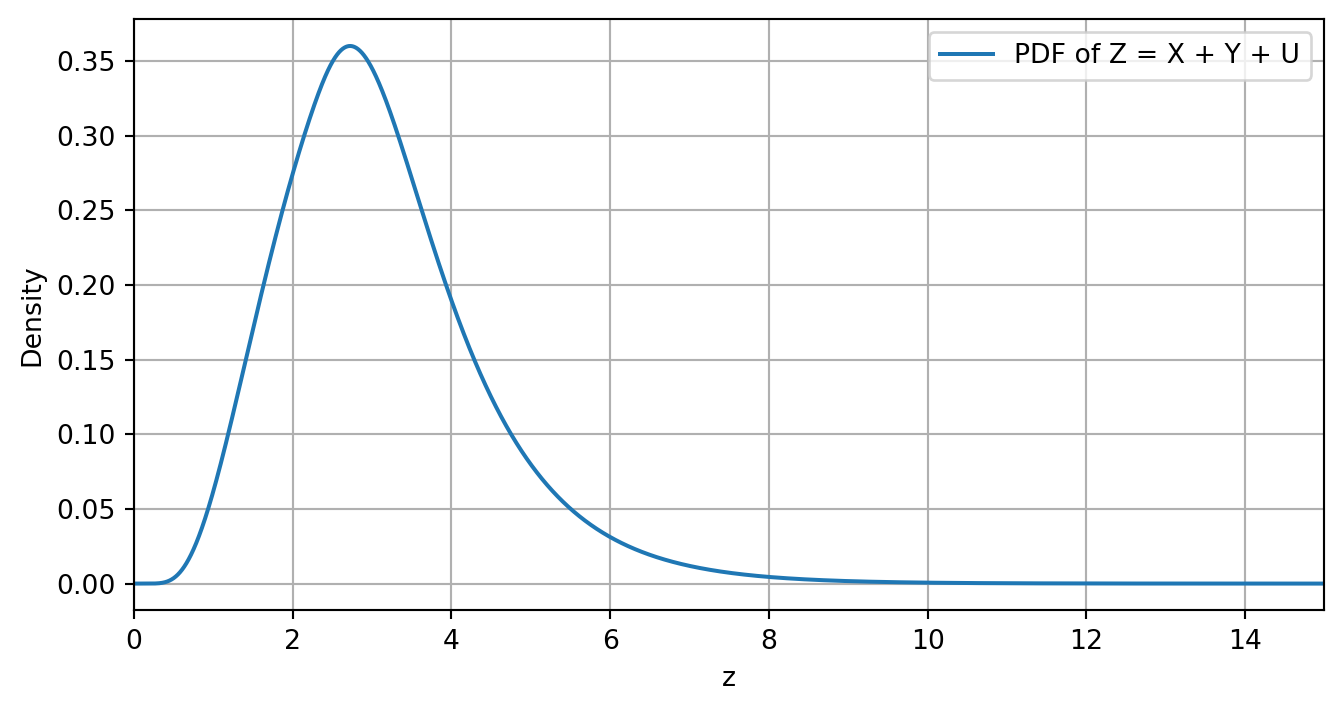

6.2 Simulation-based inference

6.2.1 Data generation

Here come general remarks about generating data (samples) from distributions.

6.2.2 Examples from Chapter 7

Here come various examples from Chapter 7.

6.3 Interactive visualizations

In this section we present various interactive visualizations that were demonstrated in class. Note that every example also contains a link to a stand-alone website with the application, in case this notebook does not format them well on your device.

These applications have been constructed using Python’s Vega-Altair package. You can access the code of all applications as well by clicking on the “Show code generating the plot below” button.

You can copy this code into a Jupyter notebook to run it yourself (although the sliders might appear at a different point in the figure). Furthmore, you might need to run the following line in the Anaconda prompt (if you are using Python via the Anaconda installation) so that the line alt.data_transformers.enable("vegafusion") in some codes does not raise an error.

conda install -c conda-forge vegafusion vl-convert-python

Example 2.33

In this section we provide an interactive application for the visualization of the bivarate Normal distribution. This tool gives the option to vary the covariance matrix entries in four different ways (each with their own characteristic). You can also control which probability contour is plotted.

The means are fixed at \mu_X = 5 and \mu_Y = 50. The reason these cannot be varied is because this only give rise to a linear translation of the elements in the application, which is mathematically not interesting.

If the app is not well-formatted on your device, you can also find it here.

import pandas as pd
import numpy as np
import altair as alt
from scipy.stats import chi2

# For Altair to handle large dataframes
alt.data_transformers.enable("vegafusion")


# Fixed mean values
mu_x = 5
mu_y = 50


# -----------------------------
# Interactive sliders
# -----------------------------
# Values of p for probability contours
p_values = np.arange(0.05, 1.0, 0.05)
 
# Slider for probability p
p_slider = alt.param(
        name="p",
        value=0.95,
        bind=alt.binding_range(min=p_values.min(), 
                               max=p_values.max(), 
                               step=0.05,
                               name="Probability contour for p = ")
)

# Different regimes for correlation/covariance
sigma_values = [(4,25,8), 
                (4,25,-8),
                (4,25,0),
                (3,6,4)]

# Dropdown menu for sigma regimes
sigma_selector = alt.param(
    name="sigma",
    value=sigma_values[0],  # Set the default value
    bind=alt.binding_select(options=sigma_values, 
                            name="Select covariance matrix σₓ, σᵧ, σₓᵧ = ")
)


# -----------------------------
# Initial data frames 
# -----------------------------
df_points = pd.DataFrame({
    "x": pd.Series(dtype="float64"),
    "y": pd.Series(dtype="float64"),
    "name": pd.Series(dtype="string"),
    "sigma": pd.Series(dtype="object"),
})

df_line = pd.DataFrame({
    "x": pd.Series(dtype="float64"),
    "y": pd.Series(dtype="float64"),
    "name": pd.Series(dtype="string"),
    "sigma": pd.Series(dtype="object"),
})

df_ellipses = pd.DataFrame({
    "x": pd.Series(dtype="float64"),
    "y": pd.Series(dtype="float64"),
    "p": pd.Series(dtype="float64"),
    "theta": pd.Series(dtype="float64"),
    "name": pd.Series(dtype="string"),
    "sigma": pd.Series(dtype="object"),
})

# -----------------------------
# Create data for frames 
# -----------------------------
for sigmas in sigma_values:  
    sigma_x = sigmas[0]
    sigma_y = sigmas[1]
    sigma_xy = sigmas[2]

    # Means and covariance
    mu = np.array([mu_x, mu_y])
    Sigma = np.array([[sigma_x, sigma_xy],
                      [sigma_xy, sigma_y]])

    # Random data
    np.random.seed(42)
    data = np.random.multivariate_normal(mu, Sigma, size=500)
    data_x, data_y = data[:,0], data[:,1]

    # Correlation line
    corr = np.corrcoef(data_x, data_y)[0,1]
    slope = corr * (np.std(data_y)/np.std(data_x))
    intercept = np.mean(data_y) - slope * np.mean(data_x)
    x_line = np.linspace(np.min(data_x), np.max(data_x), 100)
    y_line = intercept + slope * x_line

    df_points_new = pd.DataFrame({"x": data_x, 
                                "y": data_y, 
                                "name": "Generated data (points)", 
                                "sigma" : [sigmas] * len(data_x)})
    df_points = pd.concat([df_points, df_points_new],ignore_index=True)

    df_line_new = pd.DataFrame({"x": x_line, 
                                "y": y_line, 
                                "name": "Correlation (line)",
                                "sigma" : [sigmas] * len(x_line)})
    df_line = pd.concat([df_line, df_line_new],ignore_index=True)

    # Precompute ellipses for all p
    def probability_ellipse(mu, Sigma, p, n_points=200):
        c = chi2.ppf(p, df=2)
        vals, vecs = np.linalg.eigh(Sigma)
        axes = np.sqrt(vals * c)
        theta = np.linspace(0, 2*np.pi, n_points)
        ellipse = vecs @ np.vstack([axes[0]*np.cos(theta), axes[1]*np.sin(theta)])
        ellipse[0] += mu[0]
        ellipse[1] += mu[1]
        return pd.DataFrame({"x": ellipse[0], 
                            "y": ellipse[1], 
                            "theta": theta, 
                            "p": p, 
                            "name": "Probability contour (ellipse)",
                            "sigma" : [sigmas] * len(ellipse[0])}).sort_values("theta") 

    df_ellipses_new = pd.concat([probability_ellipse(mu, Sigma, p) for p in p_values])
    df_ellipses = pd.concat([df_ellipses, df_ellipses_new],ignore_index=True)

# -----------------------------
# Create the visualization
# -----------------------------
# Define the domain limits
x_min, x_max = -2, 12
y_min, y_max = 30, 70

# Info for legend
color_legend=alt.Scale(domain=["Generated data (points)", 
                               "Correlation (line)", 
                               "Probability contour (ellipse)"], 
                                   range=["grey", "red", "blue"])

# Filter points within domain
df_points_filtered = df_points[
    (df_points["x"] >= x_min) & (df_points["x"] <= x_max) &
    (df_points["y"] >= y_min) & (df_points["y"] <= y_max)
]

# Now use df_points_filtered for the data points
points = alt.Chart(df_points_filtered).transform_filter(
    (alt.datum.sigma[0] == sigma_selector[0]) & # Match with selected sigma regime
    (alt.datum.sigma[1] == sigma_selector[1]) &
    (alt.datum.sigma[2] == sigma_selector[2])
).mark_circle(size=40, opacity=0.5).encode(
    x="x:Q", y="y:Q", 
    color=alt.Color("name:N", 
                   scale=color_legend,
                   legend=alt.Legend(title="Element type"))
)

# Line can also be filtered
df_line_filtered = df_line[
    (df_line["x"] >= x_min) & (df_line["x"] <= x_max) &
    (df_line["y"] >= y_min) & (df_line["y"] <= y_max)
]

line = alt.Chart(df_line_filtered).transform_filter(
    (alt.datum.sigma[0] == sigma_selector[0]) &
    (alt.datum.sigma[1] == sigma_selector[1]) &
    (alt.datum.sigma[2] == sigma_selector[2])
).mark_line(strokeWidth=2).encode(
    x="x:Q", 
    y="y:Q",
    color=alt.Color("name:N", 
                   scale=color_legend,
                   legend=alt.Legend(title="Element type"))
)

# Ellipse can be filtered similarly
df_ellipses_filtered = df_ellipses[
    (df_ellipses["x"] >= x_min) & (df_ellipses["x"] <= x_max) &
    (df_ellipses["y"] >= y_min) & (df_ellipses["y"] <= y_max)
]

ellipse = alt.Chart(df_ellipses_filtered).transform_filter(
   (alt.datum.p - p_slider) ** 2 < 1e-6, 
    (alt.datum.sigma[0] == sigma_selector[0]) &
    (alt.datum.sigma[1] == sigma_selector[1]) &
    (alt.datum.sigma[2] == sigma_selector[2])
).mark_line(strokeDash=[5,5]).encode(
    x="x:Q", y="y:Q", order="theta",
    color=alt.Color("name:N", 
                   scale=color_legend,
                   legend=alt.Legend(title="Element type"))
)

# Combine charts
chart = (points + line + ellipse).add_params(sigma_selector,p_slider).encode(
    x=alt.X("x:Q", scale=alt.Scale(domain=[x_min, x_max])),
    y=alt.Y("y:Q", scale=alt.Scale(domain=[y_min, y_max]))
).properties(width=500, height=350, 
    title={"text": {
        "expr": 
        "'Bivariate Normal distribution with probability contour for p = ' + format(p, \".2f\")"},
            "anchor": "middle"
        }
)

chart

Example 2.50

Here we give an interactive visualizaiton of Example 2.50 illustrating the tail behaviour of the Gamma(\alpha,\beta)-Mixed Poisson distribution as \alpha varies.

If the app is not well-formatted on your device, you can also find it here.

import numpy as np
import pandas as pd
import altair as alt
from scipy.stats import nbinom

# -----------------------------
# Parameters
# -----------------------------
k2 = np.arange(0, 31)
beta_nb = 1.0
p_nb = beta_nb / (beta_nb + 1)

# Range of alpha values for slider
alpha_values = np.arange(1.0, 15.1, 0.5)

# -----------------------------
# Build DataFrame
# -----------------------------
rows = []
for alpha in alpha_values:
    pmf = nbinom(n=alpha, p=p_nb).pmf(k2)
    tail = 1 - nbinom(n=alpha, p=p_nb).cdf(k2 - 1)

    for k, p, t in zip(k2, pmf, tail):
        rows.append({
            "k": k,
            "value": p,
            "type": "PMF",
            "alpha": alpha
        })
        if k > 0:  # avoid log(0)
            rows.append({
                "k": k,
                "value": t,
                "type": "Tail",
                "alpha": alpha
            })

df = pd.DataFrame(rows)

# -----------------------------
# Slider parameter
# -----------------------------

alpha_slider = alt.param(
    name="alpha",
    value=5.0,
    bind=alt.binding_range(
        min=alpha_values.min(),
        max=alpha_values.max(),
        step=1,
        name=r"Dispersion control value α =  "
    )
)

slider_chart = (
    alt.Chart(pd.DataFrame({"x": [0]}))
    .add_params(alpha_slider)
    .mark_point(opacity=0)
    .properties(
        height=10,
        title=" "
    )
)


# -----------------------------
# PMF plot
# -----------------------------
pmf_chart = (
    alt.Chart(df[df["type"] == "PMF"])
    .transform_filter(alt.datum.alpha == alpha_slider)
    .mark_line(interpolate="step-after", strokeWidth=2, color="blue")
    .encode(
        x=alt.X("k:Q", title=r"k",scale=alt.Scale(domain=[0, 30]),
                axis=alt.Axis(
                titleFontSize=15,
                titleFontWeight='lighter')),
        y=alt.Y("value:Q", title=r"P(X = x)",scale=alt.Scale(domain=[0, 0.5]), 
                axis=alt.Axis(
                titleFontSize=15,
                titleFontWeight='lighter')
               )
    )
    .properties(
        title={"text": {
                        "expr": "'Gamma(α=' + alpha + ',β=1)-Mixed Poisson (Negative Binomial)'"
                    },
                    "anchor": "middle"
                },
        width=225,
        height=200
    )
)

# -----------------------------
# Tail probability plot (log-log)
# -----------------------------
tail_chart = (
    alt.Chart(df[df["type"] == "Tail"])
    .transform_filter(alt.datum.alpha == alpha_slider)
    .mark_line(strokeWidth=2, color="blue")
    .encode(
        x=alt.X("k:Q", title=r"k", scale=alt.Scale(type="log"),axis=alt.Axis(
                titleFontSize=15,
                titleFontWeight='lighter',
            )),
        y=alt.Y(
            "value:Q",
            scale=alt.Scale(type="log", domain=[1e-9, 1]),
            title=r"P(X ≥ x)",
            axis=alt.Axis(
                titleFontSize=15,
                titleFontWeight='lighter',
            )
        )
    )
    .properties(
        title={"text": {
                        "expr": "'Corresponding tail probability (Negative Binomial)'"
                    },
                    "anchor": "middle"
                },
        width=225,
        height=200
    )
)

# -----------------------------
# Final layout
# -----------------------------
final_chart = alt.vconcat(
    slider_chart,
    pmf_chart | tail_chart
)

final_chart

Example 4.18

Here we show the convergence of a standardized Gamma(k,1) distribution to a Normal distribution as k increases.

If the app is not well-formatted on your device, you can also find it here.

import numpy as np
import pandas as pd
import altair as alt
from scipy import stats
alt.data_transformers.enable("vegafusion")

# -----------------------------
# Slider values
# -----------------------------
k_values = np.arange(2, 100, 1)  # integer k from 1 to 15
lam = 1.0  # lambda parameter

# x-axis for standardized values
x = np.linspace(-3, 3, 100)

# -----------------------------
# Build long-form DataFrames for all k values
# -----------------------------
rows_pdf = []
rows_cdf = []

for k_slider in k_values:
    # Gamma distribution
    gamma_dist = stats.gamma(a=k_slider, scale=1/lam)
    mu = gamma_dist.mean()
    sigma = gamma_dist.std()

    gamma_pdf = gamma_dist.pdf(mu + sigma * x) * sigma
    gamma_cdf = gamma_dist.cdf(mu + sigma * x)

    # Standard Normal reference
    normal_pdf = stats.norm.pdf(x)
    normal_cdf = stats.norm.cdf(x)

    # PDF rows
    for xi, gpdf, npdf in zip(x, gamma_pdf, normal_pdf):
        rows_pdf.append({"x": xi, "value": gpdf, "distribution": "Standardized Gamma", "k_slider": k_slider})
        rows_pdf.append({"x": xi, "value": npdf, "distribution": "Normal(0,1)", "k_slider": k_slider})

    # CDF rows
    for xi, gcdf, ncdf in zip(x, gamma_cdf, normal_cdf):
        rows_cdf.append({"x": xi, "value": gcdf, "distribution": "Standardized Gamma", "k_slider": k_slider})
        rows_cdf.append({"x": xi, "value": ncdf, "distribution": "Normal(0,1)", "k_slider": k_slider})

df_pdf = pd.DataFrame(rows_pdf)
df_cdf = pd.DataFrame(rows_cdf)

# -----------------------------
# Slider parameter
# -----------------------------
k_slider_param = alt.param(
    name="k",
    value=5,
    bind=alt.binding_range(min=k_values.min(), 
                           max=k_values.max(), 
                           step=1,
                           name=r"Value k = ")
)

slider_chart = (
    alt.Chart(pd.DataFrame({"x": [0]}))
    .add_params(k_slider_param)
    .mark_point(opacity=0)
    .properties(height=10)
)

# -----------------------------
# PDF chart
# -----------------------------
pdf_chart = (
    alt.Chart(df_pdf)
    .transform_filter(alt.datum.k_slider == k_slider_param)
    .mark_line()
    .encode(
        x=alt.X("x", scale=alt.Scale(domain=[-3, 3]), title="x",axis=alt.Axis(
                    titleFontSize=15, # Size
                    titleFontWeight='lighter')),
        y=alt.Y("value", scale=alt.Scale(domain=[-0.05, 0.6]), title="f(x)", axis=alt.Axis(
                    titleFontSize=15, # Size
                    titleFontWeight='lighter')),
        color=alt.Color("distribution:N", legend=alt.Legend(title="Distribution"))
    )
    .properties(width=225, height=200, title="Probability Density Function")
)

# -----------------------------
# CDF chart
# -----------------------------
cdf_chart = (
    alt.Chart(df_cdf)
    .transform_filter(alt.datum.k_slider == k_slider_param)
    .mark_line()
    .encode(
        x=alt.X("x", scale=alt.Scale(domain=[-3, 3]), title="x",axis=alt.Axis(
                    titleFontSize=15, # Size
                    titleFontWeight='lighter')),
        y=alt.Y("value", scale=alt.Scale(domain=[-0.05, 1]), title="F(x)",axis=alt.Axis(
                    titleFontSize=15, # Size
                    titleFontWeight='lighter')),
        color=alt.Color("distribution:N", legend=alt.Legend(title="Distribution"))
    )
    .properties(width=225, height=200, title="Cumulative Density Function")
)

# -----------------------------
# Combine slider + charts
# -----------------------------
final_chart = alt.vconcat(
    slider_chart,
    pdf_chart | cdf_chart
).properties(title={
                "text": {
                    "expr": "'Standardized Gamma(k=' + k + ',1) and Normal(0,1) distribution'"
                },
                "anchor": "middle"
            })

final_chart

Example 4.28

Here we show convergence of the standardized sum of Poisson(1) random variables to a Normal distribution. Note that this concerns “convergence” of a discrete distribution to a continuous distribution.

If the app is not well-formatted on your device, you can also find it here.

import numpy as np
import pandas as pd
import altair as alt
from scipy import stats
# alt.data_transformers.enable("vegafusion") 

# -----------------------------
# Slider values
# -----------------------------
k_values = np.arange(1, 50, 1)

# -----------------------------
# Build DataFrames separately
# -----------------------------
rows_pois = []
rows_norm = []

for k in k_values:
    # --- Poisson sum ---
    pois_dist = stats.poisson(mu=k)
    multiple = 4  # This value should be the same as the x_range later one; 
                  # otherwise there are also x-values outside the plotted range 
                  # which makes the legend jump around. This is a rule of thumb, though.
    s_vals = np.arange(0, k + multiple * np.sqrt(k)) # Most mass falls in this support

    z_vals = (s_vals - k) / np.sqrt(k)
    pmf_vals = pois_dist.pmf(s_vals)

    bin_width = 1 / np.sqrt(k)

    for z, p in zip(z_vals, pmf_vals):
        rows_pois.append({
            "z": z,
            "value": p / bin_width,
            "k_slider": k,
            "legend": "Standardized Poisson Sum"
        })

    # --- Normal reference ---
    x_range = multiple
    x = np.linspace(-x_range, x_range, 100)
    normal_pdf = stats.norm.pdf(x)

    for xi, yi in zip(x, normal_pdf):
        rows_norm.append({
            "z": xi,
            "value": yi,
            "k_slider": k,
            "legend": "Normal(0,1)"
        })

df_pois = pd.DataFrame(rows_pois)
df_norm = pd.DataFrame(rows_norm)

# -----------------------------
# Slider parameter
# -----------------------------
k_slider_param = alt.param(
    name="k",
    value=1,
    bind=alt.binding_range(
        min=k_values.min(),
        max=k_values.max(),
        step=1,
        name="Value k = "
    )
)

slider_chart = (
    alt.Chart(pd.DataFrame({"x": [0]}))
    .add_params(k_slider_param)
    .mark_point(opacity=0)
    .properties(height=0)
)


# -----------------------------
# Common legend properties
# -----------------------------
color_encoding = alt.Color(
    "legend:N",
    scale=alt.Scale(
        domain=["Standardized Poisson Sum", "Normal(0,1)"],
        range=["pink", "blue"]
    ),
    legend=alt.Legend(title="Distribution", orient="right")
)

# -----------------------------
# Poisson bars
# -----------------------------
# Define the width calculation
pmf_chart = (
    alt.Chart(df_pois)
    .transform_filter(alt.datum.k_slider == k_slider_param)  # Filter based on slider value
    .mark_bar(opacity=0.7,width= 25 * k_slider_param ** (-0.5)) # Set heuristically by inspection
    .encode(
        x=alt.X("z:Q", title="Standardized value", scale=alt.Scale(domain=[-x_range, x_range]),             
                axis=alt.Axis(
                    titleFontSize=15, # Size
                    titleFontWeight='lighter')),
        y=alt.Y("value:Q", title=r"Density",
                axis=alt.Axis(
                    titleFontSize=15, # Size
                    titleFontWeight='lighter')), # Amount of bold face
        color=color_encoding
    )
)


# -----------------------------
# Normal line
# -----------------------------
normal_curve = (
    alt.Chart(df_norm)
    .transform_filter(alt.datum.k_slider == k_slider_param)
    .mark_line(size=3)
    .encode(
        x=alt.X("z:Q", scale=alt.Scale(domain=[-x_range,x_range])),
        y="value:Q",
        color=color_encoding
    )
)


# -----------------------------
# Final chart
# -----------------------------
final_chart = alt.vconcat(
    slider_chart,
    (pmf_chart + normal_curve).properties(
        title={
            "text": {
                "expr": "'Standardized sum of k = ' + k + ' Poisson(1) variables'"
            },
            "anchor": "middle"
        }, width=350, height=300
    )
)

final_chart

Example 4.29

Here we show the convergence of the sum of bimodal PDFs to a Normal distribution with the same mean and variance.

If the app is not well-formatted on your device, you can also find it here.

import numpy as np
import pandas as pd
import altair as alt
from scipy.signal import convolve
alt.data_transformers.enable("vegafusion")

def bimodal_pdf(x, mu1, sigma1, mu2, sigma2, w1, w2):
    """Compute a bimodal PDF as a weighted sum of two normal distributions."""
    pdf1 = (1 / (np.sqrt(2 * np.pi) * sigma1)) * np.exp(-0.5 * ((x - mu1) / sigma1) ** 2)
    pdf2 = (1 / (np.sqrt(2 * np.pi) * sigma2)) * np.exp(-0.5 * ((x - mu2) / sigma2) ** 2)
    return w1 * pdf1 + w2 * pdf2

def compute_convolution(pdf1, pdf2, dx):
    """Compute the convolution of two PDFs and normalize the result."""
    conv = convolve(pdf1, pdf2, mode='full') * dx
    return conv / np.sum(conv * dx)

# Parameters for the bimodal distribution
mu1, sigma1 = 2.0, 0.5
mu2, sigma2 = 6.0, 1.0
w1, w2 = 0.5, 0.5

# Compute mean and variance of the bimodal distribution
mu_bimodal = w1 * mu1 + w2 * mu2
var_bimodal = w1 * (sigma1**2 + mu1**2) + w2 * (sigma2**2 + mu2**2) - mu_bimodal**2
sigma_bimodal = np.sqrt(var_bimodal)

# Initial x range and PDF (wide enough)
x = np.linspace(-5, 25, 100)
dx = x[1] - x[0]
y = bimodal_pdf(x, mu1, sigma1, mu2, sigma2, w1, w2)

# DataFrames for Altair plotting
df_list = []
df_normal_list = []

# n values
n_values = np.arange(1, 21, 1)

for n in n_values:
    pdf_n = y.copy()
    x_n = x.copy()

    # Perform (n-1) convolutions
    for _ in range(n - 1):
        x_n_new = np.linspace(x_n[0] + x[0], x_n[-1] + x[-1], len(pdf_n) + len(y) - 1)
        pdf_n = compute_convolution(pdf_n, y, dx)
        x_n = x_n_new

    # Compute cumulative sum for approximate CDF
    cdf_n = np.cumsum(pdf_n) * dx
    # Determine 0.01 and 0.99 quantiles
    x_min = np.interp(0.0001, cdf_n, x_n)
    x_max = np.interp(0.9999, cdf_n, x_n)

    # Mask to keep only points in [x_min, x_max]
    mask = (x_n >= x_min) & (x_n <= x_max)
    x_n_trim = x_n[mask]
    pdf_n_trim = pdf_n[mask]

    # Add bimodal convolution data
    for xi, pi in zip(x_n_trim, pdf_n_trim):
        df_list.append({"x": xi, "PDF of bimodal sum": pi, "n": n, "legend": "Sum of Bimodal PDFs"})

    # Normal approximation data (same x-range)
    mu_normal = n * mu_bimodal
    sigma_normal = np.sqrt(n) * sigma_bimodal
    pdf_normal = (1 / (np.sqrt(2 * np.pi) * sigma_normal)) * np.exp(-0.5 * ((x_n_trim - mu_normal) / sigma_normal) ** 2)
    for xi, pi in zip(x_n_trim, pdf_normal):
        df_normal_list.append({"x": xi, "PDF of bimodal sum": pi, "n": n, "legend": "Normal with same mean/variance"})

# Convert to DataFrames
df = pd.DataFrame(df_list)
df_normal = pd.DataFrame(df_normal_list)

# Slider
n_selector = alt.param(
    name="n",
    value=1,
    bind=alt.binding_range(min=n_values.min(), 
                           max=n_values.max(), 
                           step=1, 
                           name="Value n = ")
)

# -----------------------------
# Common legend properties
# -----------------------------
color_encoding = alt.Color(
    "legend:N",
    scale=alt.Scale(
        domain=["Sum of Bimodal PDFs", "Normal with same mean/variance"],
        range=["pink", "blue"]
    ),
    legend=alt.Legend(title="Distribution", orient="right") 
)

# Altair plot
chart_bimodal = alt.Chart(df).add_params(n_selector).transform_filter(
    alt.datum.n == n_selector
).mark_area(opacity=0.3).encode(
    x='x:Q',
    y='PDF of bimodal sum:Q',
    color=color_encoding
)

chart_normal = alt.Chart(df_normal).transform_filter(
    alt.datum.n == n_selector
).mark_line(strokeDash=[5,2]).encode(
    x='x:Q',
    y='PDF of bimodal sum:Q',
    color=color_encoding
)

(chart_bimodal + chart_normal).properties(
    title={"text":{"expr":"'Sum of n = ' + n + ' bimodal PDFs'"},"anchor":"middle"}, width=350, height=300
)